Machine learning applied to radioactive decay data (Bachelor thesis)
Reflection Link to heading
This 6 month journey has been one with many challenges, but also one of a lot of personal growth. Life was not always easy during this semester, which had caused unfortunate delays in the project. As my supervisor assured me, this is how it always goes in research. Plans continuously change, timetables need adjusting and ambitious ideas put on hold. This project then certainly made me improve my planning skills. Dealing with setbacks was also more common in this rather independent project, compared to any coursework before.
On an intellectual level, it was a challenge in the beginning to adjust to the academic writing style of papers. Information is more dense and sometimes not explained in detail, referring the reader to some other paper. This trail of research papers that one can go down, even in a small topic as the one I was researching, is truly eye-opening to me. The amount of information that is out there is unimaginable to me. The project also introduced me to new applications of statistics and tested some old statistical knowledge, such as that on exponential distributions, statistical moments like variance and higher order ones. On top of that, I enjoyed learning about Monte Carlo simulations. I had always figured this term to sound complicated, but to learn that it is a rather easy methodology which has such strong use cases in various real-world applications was very interesting to learn. While not the main focus of my thesis, I also enjoyed researching the experimental background, of the process of superheavy synthesis and how detection is done.
Official abstract Link to heading
Experimental nuclear structure data coming from superheavy nuclei synthesis experiments often consists of correlated alpha decay chains. In the absence of neutron detectors - which would fully characterize the exit channel after the fusion-evaporation reaction - the sequence of decay energies and half-lives are the ‘fingerprint’ of the exit channel itself. Experimental data in this region is sparse, and its interpretation can be liable to error or confirmation bias. A so-called “Schmidt test” is a method for determining the congruence of correlation times for a set of measurements of one decay step. Its outcome is not always entirely conclusive, however. This study evaluates the congruence derived from the Schmidt test using Monte Carlo simulated data with various level of contamination from incongruent data. Furthermore, the study also includes the evaluation of congruence of data stemming from single decays and multi-step decay chains. A multi-layer perceptron was trained on extracted features from simulated decay chain sets with one step. The Schmidt test performs well with larger decay sets and when the half-life of the contaminating species is longer than the original species by a factor 5 or 10. However, the test performs poorly in low counting statistics, where few recorded decay times are available. The newly proposed machine learning model outperforms the Schmidt test in certain high statistics scenarios, but also fails when few decay times are available. Its performance is also poor when the half-life of the contaminant is shorter than the original half-life. The learning behaviour of the model is analysed, showing significant contributions from higher statistical moments in training. Future work involves including chain correlations across multiple steps, alpha decay energies, as well as the potential use of alternative machine learning models.
Results Link to heading
One of the key results of the thesis was the heatmap in Figure 1, showing how the amount of contamination in a decay time data set (that is, number of decay times from a species other than the one we are interested in) affects the Schmidt test and its conclusions. This was tested for various factors of contaminant half lives. The result is that the Schmidt test seems rather unsensitive to any contaminants with a half life on the same order of magnitude as the species we seek to study. This was further motivation to look beyond the Schmidt test, which solely relies on variance of the dataset, to see if other statistical methods (e.g. machine learning) could be used.
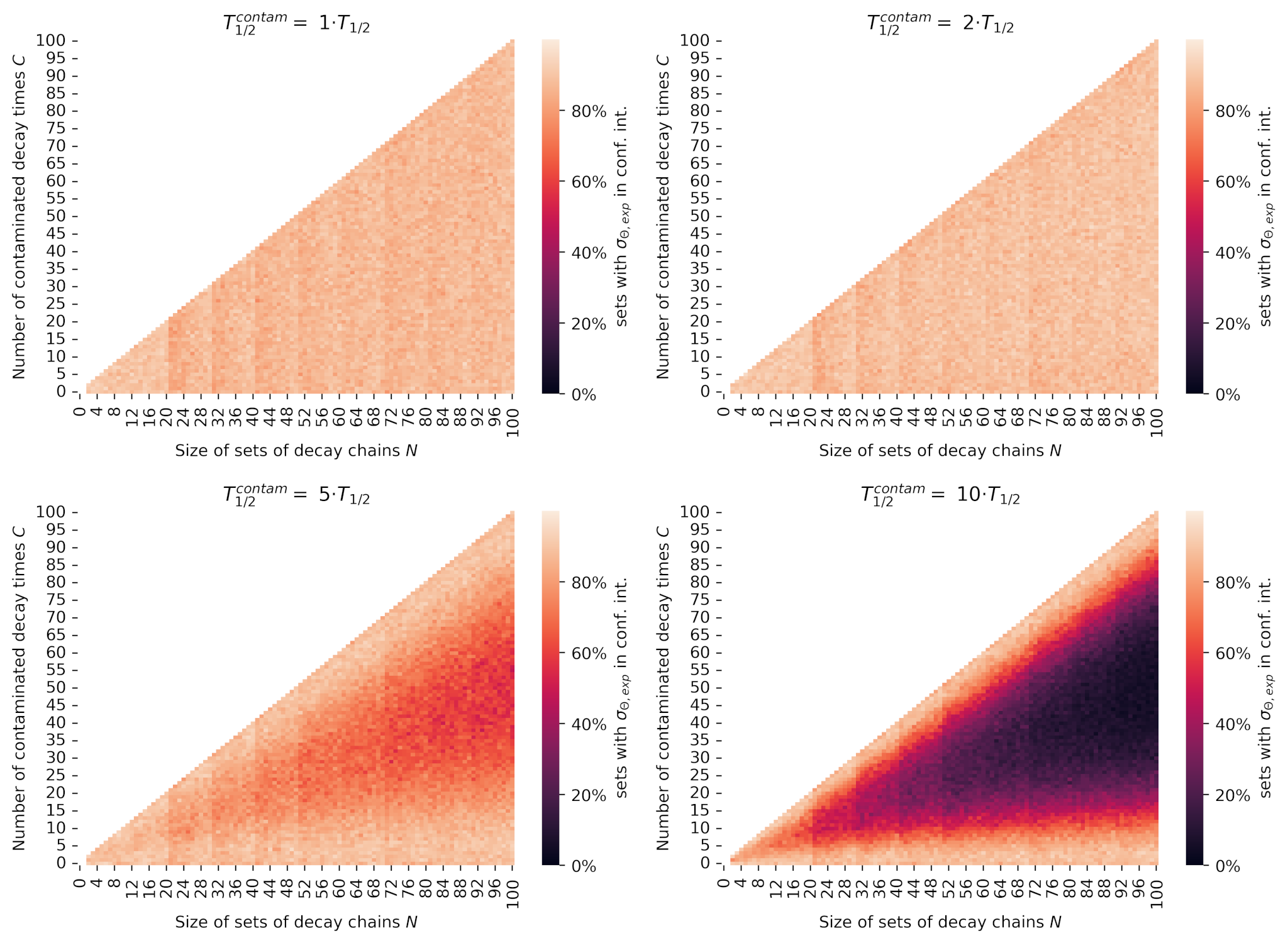
Figure 1: Heatmaps for the Schmidt test congruence for various contaminant half-lives. Each pixel is a unique combination of set size N and C contaminated decay times, where the value of the pixel represents the percentage of i=100 simulated decay chain sets with j=1 step for which the measure σ(Θ,exp) falls within the confidence interval, indicating likely congruence. The longer the contaminant half life is compared to the original, the more sets are deemed incongruent by the Schmidt test. Additionally, it can be seen that when nearly all of the decay times in the data set are from the contaminant species, the data becomes congruent again. The number of sets deemed congruent is somewhat symmetrical around the the line of 50% contamination.